比特币第二次减半将至,为什么比特币总量设置为2100万呢?这篇文章谈笑中有几分戏谑,但都是有的放矢,值得一读。
正文
比特币总量2100万个,这可能是刚接触比特币的小白们记得最清楚,也是最迷惑的数字。
中本聪没在任何公开的言论中提到:为什么选这个数字,于是网上出现了各种各样的猜测和逻辑推理。
我们就来聊聊这个数:
-
2100万是怎么来的
-
选2100万的真正原因
2100万是怎么来的
- 【1】20999999.97690000
最终产生的比特币数量,准确的说是20999999.97690000个,比2100万少一点。
比特币产生的时间表:
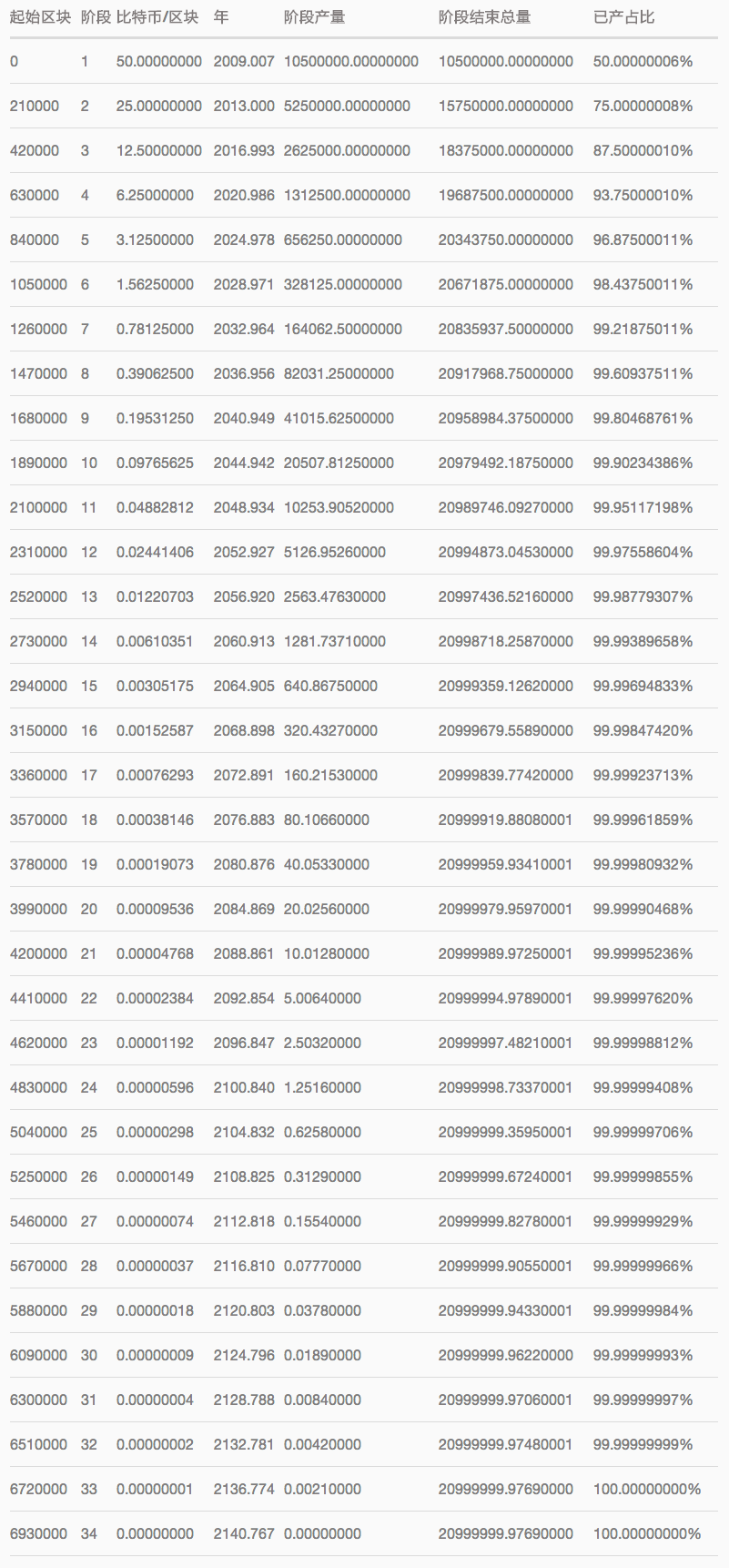
下面挑几个重点分析一下这张表。
- 【2】50.00000000
格林威治时间2009年1月3日18:15:05,创世区块诞生。创世区块的编号是0。从创世区块开始的”阶段1”,每个区块产生50个新的比特币或者说50亿聪。
创世区块:https://blockchain.info/block-height/0
- 【3】目标高度210000
格林威治时间2012年11月28日15:24:38,编号第210000个区块产生。从这个区块起的”阶段2”,每个区块包含的新比特币数量减半为25个,这是历史上第一次减半。今后每产生210000个区块,比特币数量都会依次减半。直到第33次减半时,每个块产生0.0021个新比特币直接减为0个。
210000块:https://blockchain.info/block-height/210000
- 【4】4年1次的约定
每4年减半是不太严格的说法。实际情况:比特币大约每10分钟产生一个区块,而210000个10分钟接近4年(4年等于210384个10分钟。这应该是中本聪特意选取的数字)。
- 【5】2016前,2016后
2016年将发生第二次减半,但现在讨论这个有点早。我要说的是2016个块的问题。
比特币系统调节挖矿难度的原理是:根据前2016个块产生的总时间,调整后2016个块的挖矿难度,让挖出这2016个块的时间为14天。因为,每小时6个10分钟乘以24小时再乘以14天=2016。所以,所谓10分钟只是平均值目标。由于目前算力上涨很快,实际上挖出2016个块的速度往往少于14天。
难度调整的话题涉及到挖矿,以后再一并分析。
选2100万的真正原因
网络上有很多种猜测,有些很靠谱,有些不靠谱但很欢乐。
【答案1】
It’s the first half of the answer: 42.
翻译:因为21是终极答案42的一半。
(说明:英语里,2100万表示为:21 million。所以,老外一般直接问:为啥是21。)
当然,他是开玩笑的。不过,我个人最喜欢这个猜测,这也是reddit里顶的人最多的。
这个梗来自电影《银河系漫游指南》里终极答案的桥段。
【答案2】
Because we’re living in the 21st century!
翻译:因为我们生活在21世纪!
太天真,不忍吐槽。
【答案3】
He chose a reward scheme and 10 minute blocks. When he did the math, it came to 21 million. He didn’t choose the 21 million, he just accepted the consequence of the parameters he chose.
翻译:中本聪订好10分钟、50币、4年减半的原则,结果自然出来了。他没有选,而是接受了这个自然的结果。
这个答案也是有可能的。中本聪在比特币中的很多选择确实是撞大运的,但都是“基于经验的撞大运”。
【答案4】
All gold mined in human history can be fit into a cube roughly 21 meters on each side. Satoshi created bitcoin with the idea of being sort of a digital analog of gold (finite supply, mining, etc), as well as the fact that it built upon Nick Szabo’s “Bit Gold” proposal, so I think that 21 million was sort of a clever nod to that.
翻译:全世界所有黄金熔在一起,是一个边长大约为21米的正方体。中本聪用这个概念,隐喻比特币是一种虚拟黄金。
原来阴谋论不止中国有…
【答案5】
I was going to say: Satoshi likes to play Vegas blackjack.
翻译:我觉得中本聪喜欢玩21点。
上帝玩骰子么?
【答案6】
计算机双精度浮点数最多存储2^53精度的数。而比特币按最小单位算的总精度是2^51,刚好够用。(英文太长不贴了)
这个答案,出现在一篇很不错的文章里《中本聪的天才:比特币以意想不到的方式躲开了一些密码学子弹》
详细:
比特币有争议的属性之一就是它的固定的供应量。当前每10分钟又25个新的比特币被生产出来,并且这一数字每4年减半。总的来讲,不会有超过2100万个比特币的存在。另一方面,每个比特币可以被划分成1亿份(每份叫做1“聪”),如果一美分都足够买辆车的话,用美元来交易就麻烦重重了,但比特币就算升值到和上面假设的美元的状况,也不会遇到那样的问题。因此,总之,将永远存在的货币单位的总数字是2,100,000,000,000,000,也就是2100万亿,或者说2^50.899。在选择这个数值的方面,中本聪比大多数人意识到的要幸运的多或者说聪明的多。首先,这个数字远小于2^64-1,这是一台计算机里面可以以标准整数形式存放的最大整数,超过那个值的话,数值将像里程表那样归零。 其次,然而,还有一个总“聪”数要设法低于的更小的阈值:可以用浮点的格式表示的可能的最大整数。整数不是计算机可以存储的唯一一种数字;为了处理小数,计算机使用一种做浮点表示法的格式。浮点表示法本质上就是一个科学记数法的二进制版本。举个例子,下面是一个在你学习物理学的时候会遇到的值:
地球的质量: 5.972 1024 kg
太阳的质量: 1.989 1030 kg
光速: 2.998 108 m/s
一光年: 9.460 1015 m
质子的质量: 1.672 10-27 kg
普朗克长度: 1.616 10-35 m
我们可以注意到,科学记数法是如何使得你可以在合理的精度下表示所有的这些数值,尽管它们的大小相差极大。浮点表示法本质上就是二进制的科学记数法;当你存储数字9.625的时候,你的计算机存放的是“1.001101 * 1011”(或者说,它存放的是01000000 00100011 01000000 00000000 00000000 00000000 00000000 00000000,这是高精度序列形式的同样一回事)。在这个高精度形式中,系数(也就是不是指数的那部分)有52位(52bits)。这意味着高精度(更加精确的说法是“双精度”)浮点数足以存贮高达253的数字,但不能再高了,如果超过了,你就得开始砍掉末尾的数字。比特币的2^50.9这一以指数形式表现的总“聪”数,刚好低于这个最大值。 如果我们有了整数,我们为什么还要关心浮点值呢?因为更多的高阶编程语言(比如说Javascript)并不开放低阶的“浮点”和“整数表示法”,而只给程序员提供“数”的概念 – 当然以浮点的形式提供。如果中本聪当时选择了2亿1千万而不是2100万这个值的话,用很多语言里比特币编程就会比现在要麻烦得多了。
注意,Stefan Thomas不幸的在他写BitcoinJS的时候没有及时留意到这个,以至于那个库使用了一个专门的‘大数big number’对象,而不是一个普通数来存储教程输出值;我自己分叉的的BitcoinJS(同时还加入了其他的改进)使用了普通数。
【答案7】
That explanation is close but not entirely compelling. IEEE double-precision floating-point format has 53 bits of significand precision, meaning it can address up to 253 − 1 satoshis without any rounding error. Well, that’s 9,007,199,254,740,991 satoshis, which is not anywhere close to 2,100,000,000,000,000 satoshis (or even 2,099,999,997,690,000 satoshis, which is the actual asymptotic limit). I think a much more compelling explanation is that a signed 32-bit integer can store values up to 231 − 1, which is 2,147,483,647. If you assume a fixed-point format with two decimal digits of fractional precision (which is typical for money), then a signed 32-bit integer can address up to 21,474,836.47 bitcoins, which we might as well round off to 21 million. My guess is that Satoshi derived the 21-million limit from here early in development and then later realized that this wouldn’t be enough currency units and so extended the number of decimal places from 2 to 8 and changed the variables from 32-bit to 64-bit.
翻译:答案6的解释很接近,但有点牵强。IEEE双精度浮点数是53bits,能表示的最大数是9,007,199,254,740,991聪,而比特币是2,099,999,997,690,000聪,差别还是很大的。
我觉得更好的解释:有符号32位整数可存储最大2^32-1的数,是2,147,483,647。如果比特币是小数点后两位的话,就是21,474,836.47个比特币。也就是21-million。我猜中本聪在最初开发的时候用32位精度的整数,后来发现对于一种全球通用货币来说这个精度不够,所以把小数点后2位延展成8位,从32位存储改成64位存储。
这是我觉得最靠谱的答案,因为从中本聪的过往言论可以看出,他不是一个完美主义者,而是一个实用主义者。