密钥分发的问题
在之前我们的一篇文章加密技术发展 中提到了一个经典的问题:
-
Alice和Bob是朋友,他们的住处离得比较远,Alice想要发送一则隐私消息给Bob
-
Eve想要窃听Alice和Bob的通信,Alice和Bob无法防止Eve的偷看
-
Alice把信放在一个盒子里,她上了锁,让邮差发给Bob,Eve没有钥匙,无法打开盒子,但是Bob也无法打开
那么问题来了,Alice如何把钥匙发给Bob呢?
Alice如何发送钥匙给Bob的问题,就是现代密码学中密钥分发的问题;现代密码学的大部分研究,就是围绕这个问题展开的。
我们在思想实验中虚拟了两个解决方案:
方案A
-
Alice把信息放到铁盒子里,上锁,发给Bob
-
Bob收到盒子,没有去想办法打开它,而是又加上了自己的一把锁,发回给Alice
-
Alice打开自己加的锁,发回给Bob
-
Bob打开自己的锁
方案B
-
Bob满世界散播自己的锁,随便一个人都能捡到Bob的锁并且能分辨是否被别人伪造
-
Alice捡了一把Bob的锁,把消息放进铁盒子里,锁上,发给Bob
-
Bob打开自己的锁
这两个虚拟的解决方案意义非同寻常,它证明了两个人可以互相交换秘密的信息而不怕密钥泄露;但是在真实世界中,对一则文本信息加密,并不完全像给一个铁盒子上锁那样方便,我们如何把这两个故事的寓意融入到真正的密码术当中去呢?
单向/双向函数
在密码学中,很常用的一个数学特性叫做单向函数。
同样与之相对的,还有一个概念叫做双向函数。
让我们来看看他们是什么东东。
双向函数
大部分函数都是双向函数,双向意味着可逆。比如加倍函数就是一个双向函数:
1
| |
知道了x,很容易能求得y;同理,知道了y,很容易逆向求得x。
单向函数
与上面相对的,知道x,很容易能求得y;但是知道了y,逆向很难推出x。这就是单向函数。举一个最常见的例子:
1
| |
一个很大的数的x次方来模除另一个很大的数,取模得到y,知道x,y是很容易计算的,但是反向从y推导x却十分困难。这就是一个单向函数。
码农童鞋们非常熟悉的一种算法:HASH(散列),其原理就是建立在单向函数之上的;但是现在我们先把这个应用放到一边,单单探讨单向函数在密钥交换中的作用
单向函数在密码学中的应用
Alice和Bob在不懈的努力之后,发现采用上述 M^x % P = y 的单向函数可以帮助他们交换密钥,而且 不怕遭到Eve的窃听,让我们看看他们怎么做到的:
| 选择 7^x % 11 = y 这个单向函数作为约定函数 | Alice | Bob |
|---|---|---|
| 第一步 | Alice随机选择了一个数字代入x,比如3 | Bob 随机选择了一个数字代入x,比如6 |
| 第二步 | Alice运算得到 7^3 % 11 = 2 | Bob 运算得到 7^6 % 11 = 4 |
| 第三步 | Alice把2发给Bob | Bob 把4发给Alice |
| 第四步 | Alice得到Bob发送的结果4,代入单向函数再一次运算得到 4^3 % 11 = 9 | Bob 得到Alice的2后进行同样的运算 2^6 % 11 = 9 |
神奇的事情发生了,第四步中Alice和Bob得出了相同的数字9,这个数字就是他们需要传递的密钥。
让我们再重新审视一遍,Alice和Bob在这次交换密钥的过程中都传递了什么呢?
- 他们约定了单向函数的 M, P值
- 他们各自选定了一个x值,然后计算结果y值并互相传递
- 通过前面两组信息,他们各自独立计算出了密钥值
- Eve如果监听到了M,P,以及两个人传递的y,是很难逆向计算出x,并得出密钥值的;这是单向函数的数学特性决定的
通过仔细的选定一个稳妥的单向函数,就可以通过公开的讨论来建立一个密钥。这是密码学史上一个伟大发现。它是如此的简单和违反直觉,简直让人觉得不可思议。
如果仔细看看,两个人交换模除结果y的过程,是不是和我们之前提到过的方案A有点像呢,这就是思想实验在理论世界中的映射。
这个发现是由我们前面那篇加密技术发展中帅帅的大叔们在1972年的工作成果,向他们致敬!
非对称加密算法的建立
虽然我们上面所建立的交换密钥的方案已经取得了巨大的进步,但是这个方案并不完美,因为它有一个不方便的地方:
Alice 想要给Bob发信,必须拿到Bob的y值,除非是热恋的情人,谁能一直在线回复你的消息呢?所以Alice要发信,一定要Bob配合达成一个密钥才可以;如果Bob恰巧睡觉了,这封信就只能延迟发了
这个不方便之处促使密码学家们寻求更完美的解决之道,这促成了非对称加密算法的建立。
我们至今为止的所有探讨都是建立在对称加密算法之上的。所谓对称加密,就是你有一个密钥,使用这个密钥加密一段信息,同样可以使用这个密钥解密这段信息。正是之前所有的加密算法都是建立在这个基础上的,所以密钥的传递才是如此重要。
现在让我们思考另外一种看似违反直觉的方案
如果有一种加密解密函数,它的加密密钥和解密密钥是不同的。在这个系统中,如果Alice只知道加密密钥,她只能加密,加密之后自己却无法解密–除非她知道另外一个解密密钥。
听起来好像有点绕口。用现代密码学的定义来解释,就是Alice需要同时拥有两把密钥:私钥和公钥。私钥用来解密,公钥用来加密。这样Alice只要好好藏好自己的私钥,然后把公钥广播天下,谁想要给Alice写情书,就用Alice广播出来的公钥加密寄给她就好啦,只有持有私钥的Alice才能解密这封情书。
这个系统的巨大优点就是两人通信不需要同时在线来来回回折腾了,只要两人把各自把自己的公钥广而告之,任何一个人就可以毫不顾忌的用公钥加密,写一些只能给Alice和Bob才能解密的隐私信息了。
这个方案是由帅帅的Whtfield Diffie想到的,在此我们要撒一把狗粮;这位老兄灵光一现想到这个方案之后,第一个想要与之分享的人是他的妻子玛丽,当时的情形是这样的:
那是在下午发生的,维特不得不等几个小时,玛丽才会回来。 “维特等在门口,”玛丽回忆说,”他说有事要告诉我,他脸上的表情很奇怪。我进了门,他说:’请坐下来,我想和你说话。我相信我有一个重大的发现—我是第一个知道这问题答案的人。’那一刻我感觉时间突然停止了,我似乎生活在好莱坞的电影中。”
好,单身狗童鞋们从暴击伤害中回过神来没有,让我们继续艰难的人生~~~
虽然Whtfield Diffie早在1975年就提出了这个方案,但是他没有找到他所需要的函数。他公开发表了论文,号召同时代的数学家们一起来找;但是时间飞逝,年底还是没人能找到这样的函数,有些人灰心了;正在这时,远在5000公里之外的美国西海岸,有个小组找到了这样的函数~~~这就是今天大名鼎鼎的RSA算法的诞生。
那些个帅帅的大叔们

额,关于RSA算法,阮一峰老师的文章写的更清晰,我就不多废话了;童鞋们可以移步这里来探讨细节,当然,懒得去理解数学原理对于我们下面的探讨也没啥影响~~~~
让我们总结一下一个典型的非对称加密算法的特点,并看看它是如何应用到实际中的
- Bob手里有两把钥匙,一把是公钥,另一把是私钥。有了私钥能推导出公钥,有了公钥不能推导出私钥
- 用私钥加密,可以使用公钥解密
- 用公钥加密,可以使用私钥解密
- Bob把公钥送给他的朋友们—-Alice, Sam ~~每人一把;或者直接把公钥公示在自己的个人网页上,谁都能看;
- Alice要给Bob写一封保密的信。她写完后用Bob的公钥加密,就可以达到保密的效果。
- Bob收信后,用私钥解密,就看到了信件内容。这里要强调的是,只要Bob的私钥不泄露,这封信就是安全的,即使落在别人手里,也无法解密。
- Bob给Alice回信,决定采用”数字签名”。他写完后先用Hash函数,生成信件的摘要(digest)。
- 然后,Bob使用私钥,对这个摘要加密,生成”数字签名”(signature)。Bob将这个签名,附在信件下面,一起发给Alice。
- Alice收信后,取下数字签名,用Bob的公钥解密,得到信件的摘要。由此证明,这封信确实是鲍勃发出的。
- Alice再对信件本身使用Hash函数,将得到的结果,与上一步得到的摘要进行对比。如果两者一致,就证明这封信未被修改过。
- 复杂的情况出现了。Eve想欺骗Alice,他偷偷使用了Alice的电脑,用自己的公钥换走了鲍勃的公钥。此时,Alice实际拥有的是Eve的公钥,但是还以为这是Bob的公钥。因此,Eve就可以冒充Bob,用自己的私钥做成”数字签名”,写信给Alice,让Alice用假的Bob公钥进行解密。
- 后来,Alice感觉不对劲,发现自己无法确定公钥是否真的属于Bob。每次都去寻找Bob的个人网页去比对也很麻烦;她想到了一个办法,要求Bob去找”证书中心”(certificate authority,简称CA),为公钥做认证。证书中心用自己的私钥,对Bob的公钥和一些相关信息一起加密,生成”数字证书”(Digital Certificate)。
- Bob拿到数字证书以后,就可以放心了。以后再给Alice写信,只要在签名的同时,再附上数字证书就行了。
- Alice收到信后,用CA的公钥解开数字证书,就可以拿到Bob真实的公钥了,然后就能证明”数字签名”是否真的是Bob签的。
- 以上过程涉及了
非对称加密,HASH,签名,Digest,CA等等名词,没错,我们说的就是HTTPS
完整的资料参看这里:
http://www.youdzone.com/signature.html
椭圆曲线ECC加密算法(Elliptic Curve Cryptography)
我们看到了,非对称加密的核心,依赖于一个非常健壮的单向函数。RSA采用的是大素数分解的单向函数。这基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难。大质数分解问题一直是数学里面的热门问题。
即便如此,因式分解在位对位基础里不是最难的问题。这些因式分解算法随着被因式分解的数字变得越大而变得越有效率。因式分解大批数字和乘以大批数字的难度的差距随着数字(即秘钥的字节长度)变大而缩小。随着有效解码数字的资源增加,秘钥的大小必须更快增长。对限制计算能力的手机和低功率设备来说,这不是一个可持续的情况。从长期来看,因式分解和乘法的差距是不可持续的。
所有这一切意味着RSA不是理想的系统对将来的密码学来说。在一个完美的trapdoor函数里,对于数字大小的问题,简单方法和困难方法都一同样的速率变难。所以我们需要一个基于更好的trapdoor的公钥系统。
以上RSA的这些不完美加速了另外一种算法的诞生:在1985年,加密算法被提议以一个叫椭圆曲线的数学密码分支为基础。这也是比特币地址采用的核心加密方法。
什么是椭圆曲线
对于我们小白来说,椭圆曲线可以暂时简单的理解为描述了特定点的集合的公式:
1
| |
取不同的a值和b值,这个函数在坐标轴上绘制出来的曲线大概是这样的:

a和b的取值变化决定了曲线在坐标系上的不同形状。从图中可以看到,椭圆曲线是相对X轴对称。
通过椭圆曲线乘法可以从私钥计算得到公钥,这是不可逆转的过程:K = k * G 。其中k是私钥,G是被称为生成点的常数点,而K是所得公钥。其反向运算,被称为“寻找离散对数”——已知公钥K来求出私钥k——是非常困难的。椭圆曲线乘法是密码学家称之为“陷阱门”功能的一种函数:在一个方向(乘法)很容易做,而不可能在相反的方向(除法)做。 私钥的所有者可以容易地创建公钥,然后与世界共享,知道没有人可以从公钥中反转函数并计算出私钥。
secp256k1椭圆加密曲线
a和b的不同取值可以画出多条不同的曲线,比特币使用了secp256k1标准所定义的一种特殊的椭圆曲线和一系列数学常数。该标准由美国国家标准与技术研究院 (NIST)设立。secp256k1曲线由下述函数定义,该函数可产生一条椭圆曲线:
1
| |
看到了吧,这个函数结合了我们之前介绍的取模操作和椭圆曲线函数。
上述素数p取模表明该曲线是在素数阶p的有限域内,也写作Fp,其中p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1, 这是个非常大的素数。 因为这条曲线被定义在一个素数阶的有限域内,而不是定义在实数范围,它的函数图像看起来像分散在两个维度上的散落的点,因此很难可视化。不过,其中的数学原理与实数范围的椭圆曲线相似。
这条曲线画出来的样子大概是这样的:
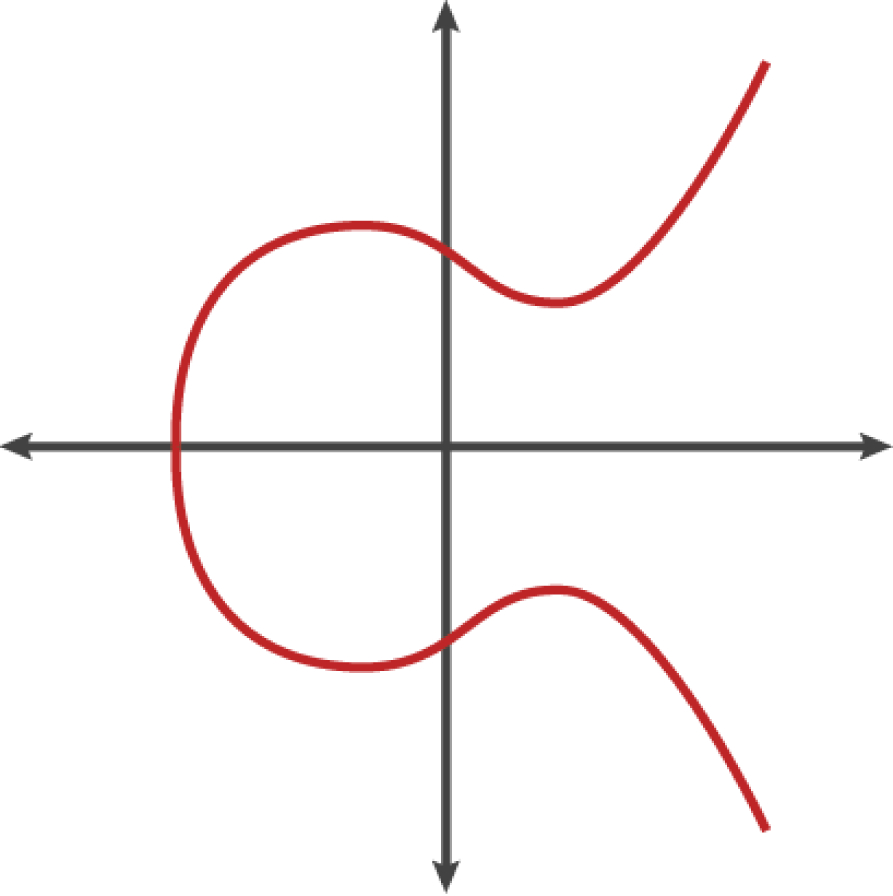
在椭圆曲线的数学原理中,有一个点被称为“无穷远点”,这大致对应于0在加法中的作用。计算机中,它有时表示为X = Y = 0(虽然这不满足椭圆曲线方程,但可作为特殊情况进行检验)。
还有一个 + 运算符,被称为“加法”,就像小学数学中的实数相加。给定椭圆曲线上的两个点P1和P2,则椭圆曲线上必定有第三点 P3 = P1 + P2。 几何图形中,该第三点P3可以在P1和P2之间画一条线来确定。这条直线恰好与椭圆曲线相交于另外一个地方。此点记为 P3’= (x,y)。然后,在x轴做翻折获得 P3=(x,-y)。
下面是几个可以解释“穷远点”之存在需要的特殊情况。
若 P1和 P2是同一点,P1和P2间的连线则为点P1 的切线。曲线上有且只有一个新的点与该切线相交。该切线的斜率可用微积分求得。即使限制曲线点为两个整数坐标也可求得斜率!
在某些情况下(即,如果P1和P2具有相同的x值,但不同的y值),则切线会完全垂直,在这种情况下,P3 = “无穷远点”。
若P1就是“无穷远点”,那么其和 P1 + P2= P2。类似地,当P2是无穷远点,则P1+ P2 = P1。这就是把无穷远点类似于0的作用。 事实证明,在这里 + 运算符遵守结合律,这意味着(A+B)+C = A+(B+C)。这就是说我们可以直接不加括号书写 A + B + C,而不至于混淆。 因此,我们已经定义了椭圆加法,我们可以对乘法用拓展加法的标准方法进行定义。给定椭圆曲线上的点P,如果k是整数,则 kP = P + P + P + …+ P(k次)。注意,在这种情况下k有时被混淆而称为“指数”。
生成公钥
以一个随机生成的私钥k为起点,我们将其与曲线上预定的生成点G相乘以获得曲线上的另一点,也就是相应的公钥 K。生成点是secp256k1标准的一部分,比特币密钥的生成点都是相同的:
{K = k * G}
其中k是私钥,G是生成点,在该曲线上所得的点K是公钥。因为所有比特币用户的生成点是相同的,一个私钥k乘以G将 得到相同的公钥K。k和K之间的关系是固定的,但只能单向运算,即从k得到K。这就是可以把比特币地址(K的衍生) 与任何人共享而不会泄露私钥(k)的原因。
提示 因为其中的数学运算是单向的,所以私钥可以转换为公钥,但公钥不能转换回私钥。
为实现椭圆曲线乘法,我们以之前产生的私钥k和与生成点G相乘得到公钥K:
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G
公钥K 被定义为一个点 K = (x, y):
K = (x, y)
其中,
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
为了展示整数点的乘法,我们将使用较为简单的实数范围的椭圆曲线。请记住,其中的数学原理是相同的。我们的目标是找到生成点G的倍数kG。也就是将G相加k次。在椭圆曲线中,点的相加等同于从该点画切线找到与曲线相交的另一 点,然后翻折到x轴。
下图显示了在曲线上得到 G、2G、4G 的几何操作。
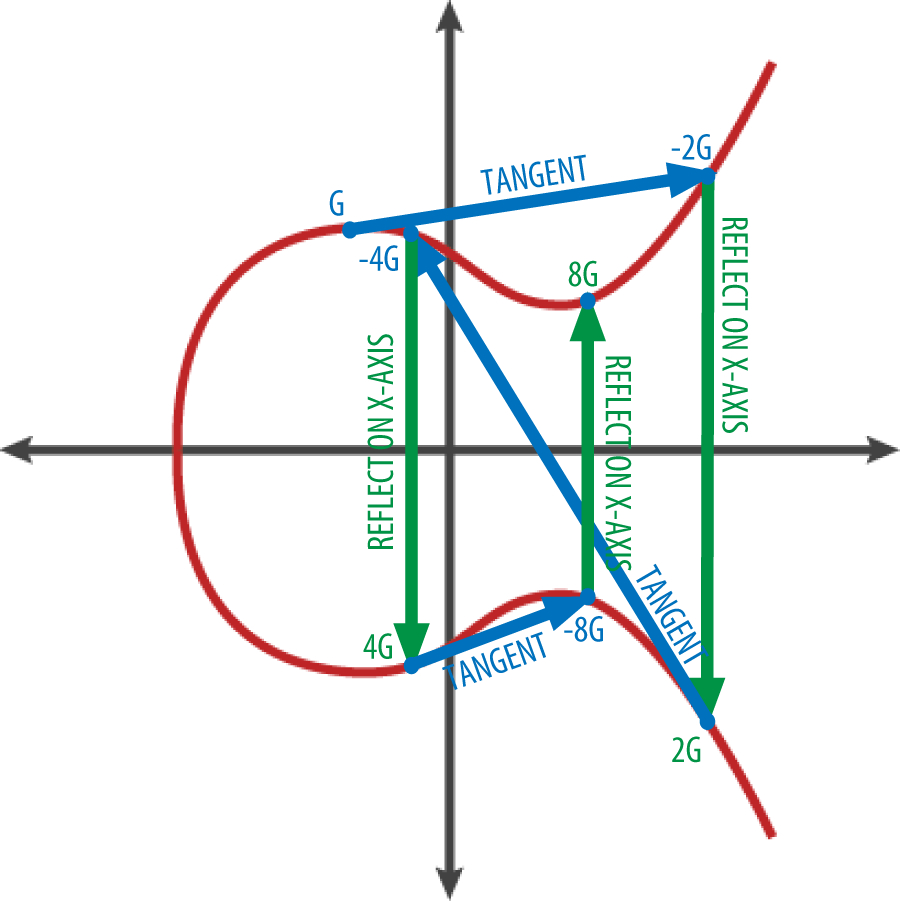
比特币账户
呼呼,以上就是比特币的账户核心算法的一部分。
- 选定了secp256k1算法,其实是通用的椭圆曲线的特化(a=0, b=7),另外选定一个非常大的模除数字p
- 选定了一个G点;G = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
- 随机生成了一个私钥k
- 求得公钥K = k * G,这里对G进行了k次翻转,一个不可逆的操作得到公钥K
- 对K再做后续变形,最终得到比特币账户的地址,这个变形又是一系列神操作,我们在后面的文章会讲
寻求更极限的安全
到目前为止,密码学家们为了实现更安全的非对称加密算法,探索了模除、大素数分解、以及椭圆曲线;他们的共同特点就是逆向运算极难极难;但是极难并不代表着不可能,随着量子计算的发展,谁也不能保证今后逆向运算的复杂度会不会有大幅降低;所以寻求更安全的单向函数始终是密码学家们最重要的工作之一;
近年来,这个探索的边界又有了更大的突破,就是为人们所熟知的量子加密技术。
限于篇幅,我们就不做更多的科普了,可以参考这本书:
https://book.douban.com/subject/1036413/
PS:一个小科普,量子计算机和量子加密其实没有多大关系哦,他们之间其实是雷锋和雷峰塔的关系,就是名字相似而已,可不要被忽悠哦
总结
呼呼,老实说,我最初想要介绍的是比特币HD钱包的演化过程,BIP32,BIP44,BIP49,BIP84以及BIP141这些文档共同定义了比特币HD钱包的底层构造。
从BIP44开始,比特币账户的管理其实已经在中本聪最初定义的一个简单地址生成的路上又走了很远;我也觉得HD钱包是比特币社区为区块链技术贡献的一个非常重要、非常有用的部分;这个钱包生成的技术超出了比特币本身,在可见的未来,会在多个领域发挥巨大作用。
为了学习比特币HD钱包的基础理论支撑,我们从最原始的凯撒加密,到Alice和Bob的思想实验,到单向函数,再到安全的密钥分发方法,到非对称加密,椭圆曲线,甚至还隐约看到了量子加密,这一切的一切是近2000年来无数密码学家们日日夜夜的冥思苦想的成果;
然后站在所有这些成果的基础上,到了中本聪及比特币技术社区手中融合发扬光大;创造了独一无二的电子货币金融账户;这个账户设计的方法之精妙,值得我们再长篇大论一番;那么,下次文章再见。
参考资料:
https://book.douban.com/subject/30280401/
https://book.douban.com/subject/1036413/