Living a Simple Life is a Happy Life

有饭吃，自由自在，就非常开心

比特币的HD钱包演化-3

| Comments

通过前面两篇文章，我们认识到比特币的所有权是通过私钥来确定的。

那么我们就在此基础上研究比特币钱包的构成。广义上，钱包是一个应用程序，为用户提供交互界面。钱包控制用户访问权限，管理密钥和地址，跟踪余额以及创建和签名交易。 狭义上，比特币钱包的核心就是对私钥的管理。

在比特币的历史发展中，钱包大致经过了三次进化:

  1. 非确定性（随机）钱包

  2. 确定性（种子）钱包

  3. 分层确定性钱包（HD Wallets (BIP-32/BIP-44)）

下面我们就好好说说钱包的历史发展轨迹

非确定性（随机）钱包

在比特币刚诞生时，Bitcoin Core客户端实现了第一个钱包功能，当时因为早期的用户并不多且都是专业人士，钱包只是随机生成的私钥集合。这种类型的钱包被称作零型非确定钱包。具体的实现细节就是: 比特币核心客户端预先生成100个随机私钥，每个密钥只使用一次；用完之后再生成100个；

这样做的缺点十分明显：

如果你生成很多私钥，你必须保存它们所有的副本。这就意味着这个钱包必须被经常性地备份。每一个密钥都必须备份，否则一旦钱包不可访问时，钱包所控制的资金就付之东流。这种情况直接与避免地址重复使用的原则相冲突——每个比特币地址只能用一次交易。地址重复使用将多个交易和地址关联在一起，这会减少隐私。

当比特币用户群逐渐扩大时，不少人因为随机生成的100个私钥用完后，没有备份老钱包，生成新的私钥后原先的钱包弃用，造成了未花费币的丢失。现在看看是个不可思议的幼稚的BUG，但是在比特币蛮荒时代，这种漫不经心的错误导致的丢币比比皆是。

确定性（种子）钱包

比特币私钥可以用任意方法生成，自然也可以通过一个随机短语进行多次hash得到不同的私钥。这种思路下，社区提出了确定性（种子）钱包的方案。

确定性，或者“种子”钱包包含通过使用HASH函数而可从公共的种子生成的私钥。种子是随机生成的数字。在确定性钱包中，种子足够恢复所有的已经产生的私钥，所以只用在初始创建时的一个简单备份就足以搞定。并且种子也足够让钱包导入或者导出。这就很容易允许使用者的私钥在钱包之间轻松转移。

比如，我们上一篇文章中用satoshi作为种子，得到SHA256(‘satoshi’)作为私钥，完全可以继续用SHA256(SHA256(‘satoshi’))…这样推导下去得出更多的私钥，同时，只需要记住satoshi这个种子，就可以方便的导入导出私钥。更进一步，可以加入password和更多的混淆短语，提高私钥生成的健壮性。

这种方案提出后，因为简单易行，多个轻钱包都做了自己的实现；虽然原理相似，但是他们之间并不通用，所以不同的钱包私钥导入导出还有一些不方便。社区就在此基础上继续探索，最终整理形成了BIP32、BIP39、BIP43，BIP44等规范，创造了我们今天通用的HD钱包。

分层确定性钱包（Hierarchical Deterministic wallet–HD Wallet）

首先用一张经典的图来描述HD钱包的私钥生成:

img

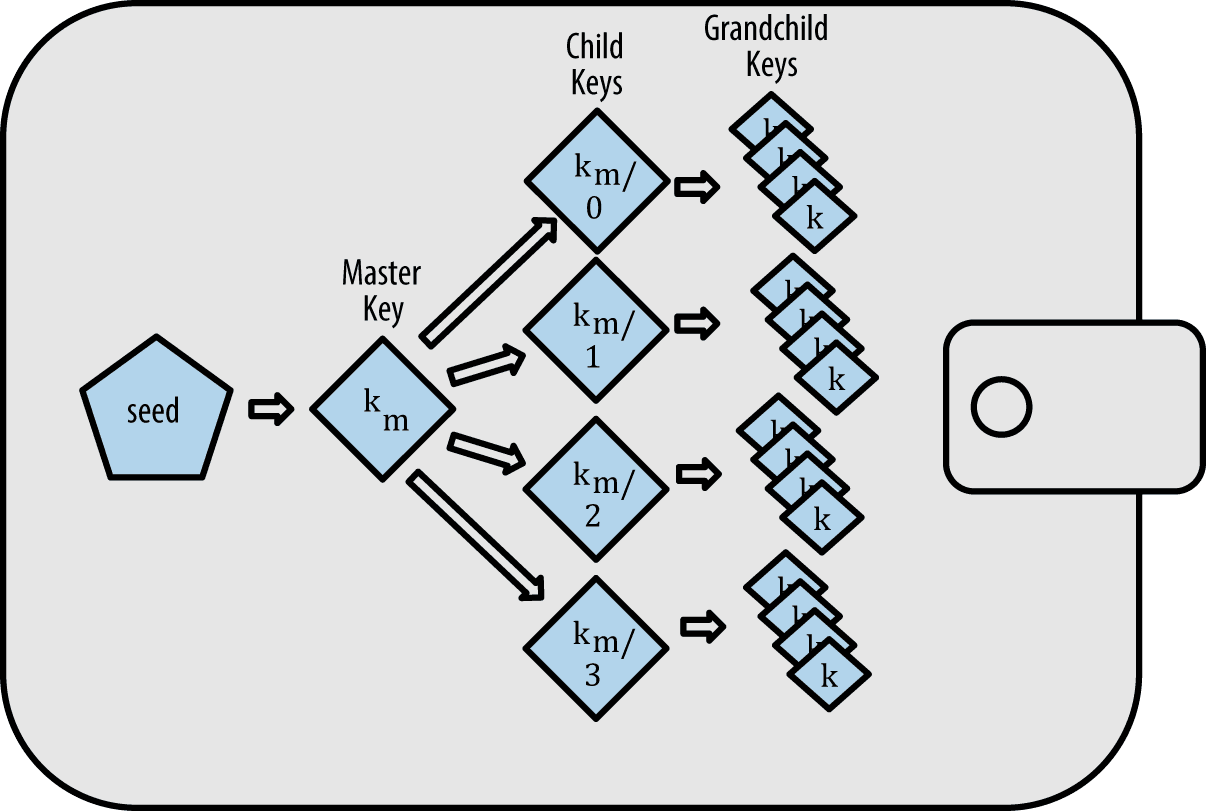
分层钱包说白了，就是将seed->私钥的过程变成了，助记词->seed->一级私钥->二级私钥->三级私钥....，即多层树状私钥生成的方案。HD钱包包含以树状结构衍生的密钥，使得父密钥可以衍生一系列子密钥，每个子密钥又可以衍生出一系列孙密钥，以此类推，无限衍生。HD钱包有两个主要的优势。

  1. 树状结构可以被用来表达额外的组织含义。比如当一个特定分支的子密钥被用来接收交易收入并且有另一个分支的子密钥用来负责支付花费。不同分支的密钥都可以被用在企业环境中，这就可以支配不同的分支部门、子公司、具体功能以及会计类别。

  2. 它可以允许使用者去建立一个公共密钥的序列而不需要访问相对应的私钥。这可允许HD钱包在不安全的服务器中使用或者在每笔交易中发行不同的公钥。公钥不需要被预先加载或者提前衍生，而在服务器中不需要存储私钥。

再来一个在线工具用于验证:

https://iancoleman.io/bip39/

最初的私钥seed来源于一个助记词（又称为Mnemonic Code），为了便于在不同的钱包中转移、导出和导入，社区对助记词的长度，范围，变换标准等等做了详尽的描述，最终形成了BIP39规范。这个规范由Trezor硬件钱包背后的公司提出，已经成为事实上的行业标准。

BIP-39定义了助记符码和种子的创建， 为了清楚起见，该过程分为两部分：

先是创建助记词，然后是从助记词到种子。下面我们从一个ffffffffffffffffffffffffffffffff 的128bits 熵开始，演示HD钱包是如何生成、管理私钥的。让我们一步一步解释。

先看看创建助记词的部分

生成步骤

  • 1、创建一个128到256位的随机序列（熵）。我们取ffffffffffffffffffffffffffffffff，称之为原始熵。

  • 2、用SHA256 HASH原始熵，就可以创造一个随机序列的校验和。代码如下

1
2
3
4
5
6

from binascii import unhexlify
from hashlib import sha256
data = 'f' * 32
data_unhexlify = unhexlify(data)
h = hashlib.sha256(data_unhexlify)
checksum = bin(int(h, 16))[2:].zfill(256)[:len(data) * 8 // 32]

得到checksum为0101

  • 3、首先求得原始熵的二进制表示，然后将校验和添加到随机序列的末尾。代码如下:
1
2
3
4
5

from binascii import unhexlify, hexlify
data = 'f' * 32
data_unhexlify = unhexlify(data)
body = bin(int(hexlify(data), 16))[2:].zfill(len(data) * 8)
final_result = body + checksum

得出的结果为

1

111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111110101
  • 4、将序列划分为包含11位的不同部分。
1

11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111111111 11111110101
  • 5、将每个包含11位部分的值作为下标索引，与一个已经预先定义2048个单词的字典做对应。BIP39中对应的字典文件可以参考这里:

https://github.com/trezor/python-mnemonic/tree/master/mnemonic/wordlist

以上二进制表示的下标值为:

1

2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2037

为什么单词数目是2048呢？ 其实seed可以有12-24个单词，所有的组合可能性为 2048^12 – 2048^24；

还记得我们之前的文章吗？比特币公钥->地址的倒数第二步是RIPEMD160，他一共有2^160可能性，上面seed的生成空间覆盖了RIPEMD160的生成空间。

  • 6、生成的有顺序的单词组，就是助记码(Mnemonic Code)。在咱们的例子中如果采用英文字典，对应的结果为:
1

zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong

一张图展示熵如何生成助记词:

img

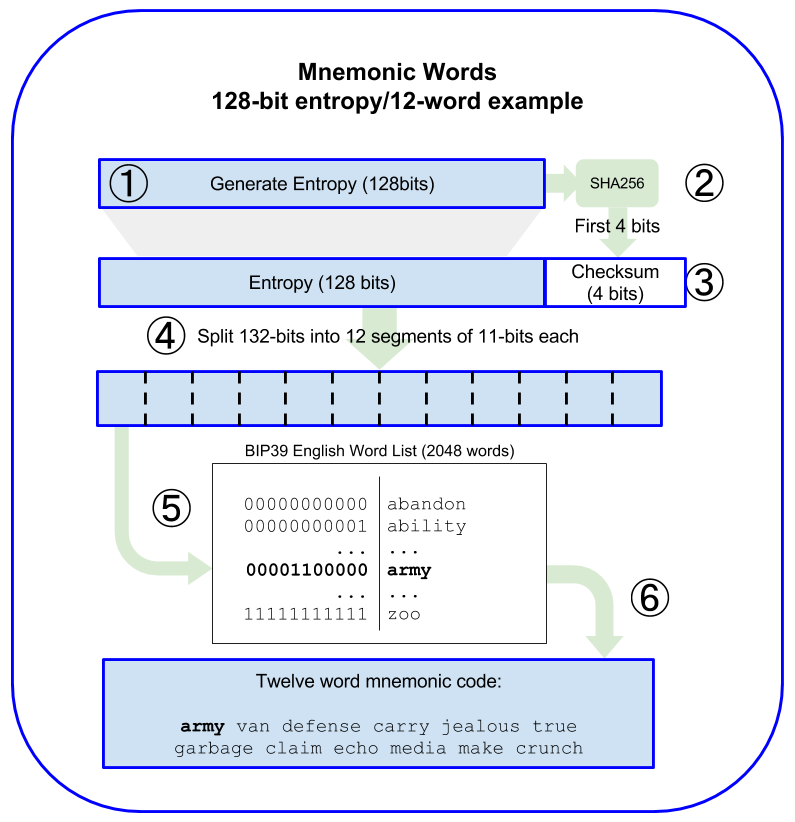
在上面这个例子中，我们选取了128Bits 原始熵，BIP39规范中，用户有128bits, 160bits, 192bits, 224bits, 256bits多个选择;下面的表格说明了熵数据的大小和助记词的长度之间的关系:

Entropy(bits) Checksum(bits) Entropy + checksum(bits) Mnemonic length(words)
128 4 132 12
160 5 165 15
192 6 198 18
224 7 231 21
256 8 264 24

目前最流行的实现还是跟我们上面的例子一样，选取128bits->12words 的Mnemonic code生成。

从助记词生成种子

现在我们已经从ffffffffffffffffffffffffffffffff随机熵得到了助记码zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong，现在需要从助记码再生成种子。

PBKDF2函数

这里我们需要先介绍一个函数:PBKDF2(Password-Based Key Derivation Function)，它是一个用来导出密钥的函数，常用于生成加密的密码。

它的基本原理是通过一个伪随机函数（例如HMAC函数），把明文和一个salt值作为输入参数，然后重复进行运算，并最终产生密钥。

如果重复的次数足够大，破解的成本就会变得很高。而salt值的添加也会增加“彩虹表”攻击的难度。

嗯，我们还要稍微解释一下HMAC的意义:

为了防止黑客通过彩虹表根据哈希值反推原始口令，在计算哈希的时候，不能仅针对原始输入计算，需要增加一个salt来使得相同的输入也能得到不同的哈希，这样，大大增加了黑客破解的难度。

如果salt是我们自己随机生成的，通常我们计算MD5时采用md5(message + salt)。但实际上，把salt看做一个“口令”，加salt的哈希就是：计算一段message的哈希时，根据不通口令计算出不同的哈希。要验证哈希值，必须同时提供正确的口令。

采用不同的hash算法时如何混入salt，可能大家八仙过海各显神通；后来为了统一化，有人提出了Hmac算法：Keyed-Hashing for Message Authentication。它通过一个标准算法，在计算哈希的过程中，把salt混入计算过程中。

简而言之，HMAC提供了标准的在HASH过程中混入salt的方法。 HMAC方法适用于任意HASH函数。

而比特币私钥生成过程中采用的PBKDF2算法，大量使用HMAC-SHA512算法，使用2048次 HASH来延伸助记符和salt参数，产生一个512位的值作为其最终输出。

这个512位的值就是种子。

利用PBKDF2从助记词得到种子步骤

1、PBKDF2密钥延伸函数的第一个参数是从步骤6生成的助记符(zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong)。

2、PBKDF2密钥延伸函数的第二个参数是salt。 由字符串常数“助记词”与可选的用户提供的密码字符串连接组成 (zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong + test)。

3、PBKDF2使用HMAC-SHA512算法，使用2048次哈希来延伸助记符和salt参数，产生一个512位的值作为其最终输出。 这个512bits的值就是种子:

1
2
3
4
5
6
7
8
9
10
11

> import hashlib
> import hmac
> from pbkdf2 import PBKDF2
> from binascii import hexlify
> PBKDF2_ROUNDS = 2048
> mnemonic = "zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong"
> passphrase = "test"
> seed = PBKDF2(mnemonic, 'mnemonic' + passphrase, iterations=PBKDF2_ROUNDS, macmodule=hmac, digestmodule=hashlib.sha512).read(64)
> print(hexlify(seed))

b'0d756ad408b442341ec4895e854fe5ee55d2a93c6544d3e77b073100e9739e35b897b3fc81ef622babd3f6d7347af2e870de86587b2663c462dd9425d3d3ef04'

从种子中创造HD钱包

我们已经得到了一个512bits的种子，我们把这个种子称之为根种子(root seed)。这个根种子是下面一切私钥产生的源泉。

让我们再回忆一下最开始的一张示意图：所有的私钥是成树状结构的。树的每一层都有无限分支，然后每一个分支都可以派生出下一层，这个结构该如何从根种子来构建呢？

这是一个精妙的设计。下面我们还是采用步步为营的方法来演示一遍:

私有子密钥的衍生

  • 1、 首先我们需要安装一个BIP32 Python解析库pip install bip32utils:

https://pypi.org/project/bip32utils/

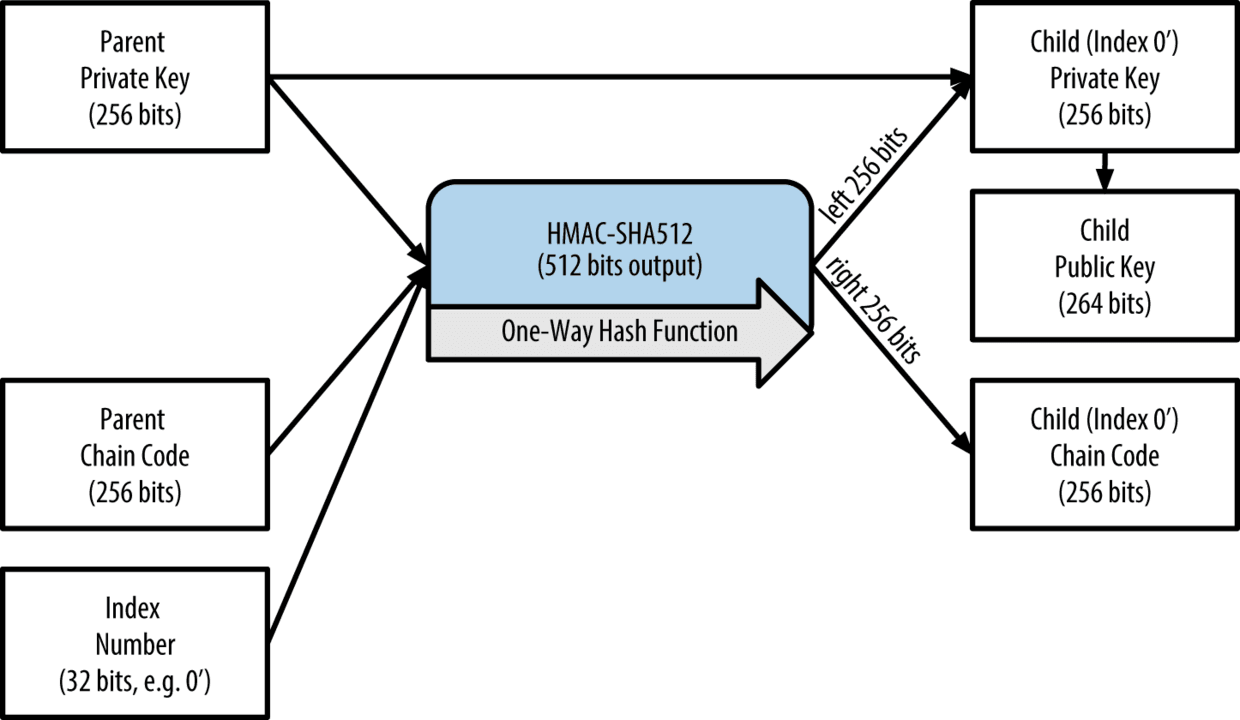
  • 2、 根种子输入到HMAC-SHA512中，得到一个512bits的输出:
1
2
3
4
5

> import binascii
> import hmac
> seed = b'0d756ad408b442341ec4895e854fe5ee55d2a93c6544d3e77b073100e9739e35b897b3fc81ef622babd3f6d7347af2e870de86587b2663c462dd9425d3d3ef04'
> entropy = binascii.hexlify(seed)
> I = hmac.new(b"Bitcoin seed", entropy, hashlib.sha512).digest()
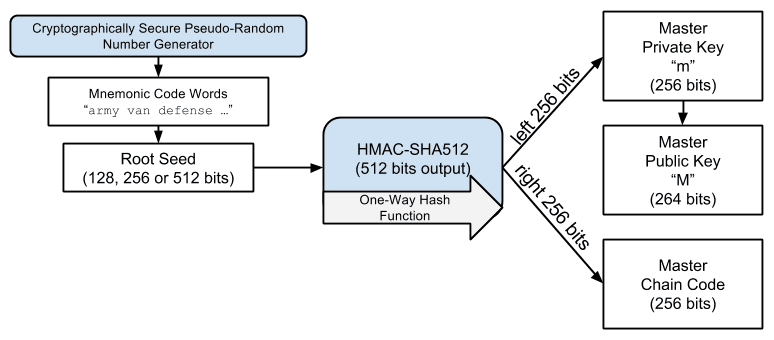
  • 3、 这个512bits的I可以分为两个部分，左边的256bits用作Master Private Key，右边的256bits用作Master Chain Code。Master Private Key又可以推导出Master Public Key。整个表示如下:

img

  • 4、 这样我们从一个512bits的输出里面分成了两个变量: Master Pirvate Key以及Master Chain Code；下面分别说说他们的作用

    • Master Private Key: 又被称作母私钥，很明显的，它可以衍生出公钥以及地址；但是我们的需求是生成多个公私钥对，所以我们又引入了一个索引号(32 bits)的概念，这样，一个母私钥+索引号，就可以生成2^31个子私钥，2^31是整个2^32范围可用的一半，因为另一半是为特定类型的推导而保留的，我们将在稍后讨论。

    • Master Chain Code: 有了Master Private Key，可以在这一层生成2^31个子私钥，但是这样无法得到我们想要的分层结构；于是就需要Master Chain Code的帮忙。这样上面的步骤我们需要三个输入：将Master Chain Code和Master Private Key以及索引号作为HMAC-SHA512的输入，又可以得到一个512bits的输出，左边的256bts就是我们需要的子私钥；重复这个过程，我们就得到了一个分层的私钥结构

  • 5、让我们总结一下这个过程:

    • 每次HMAC-SHA512，都得到一对Master Private Key以及Master Chain Code，再加上引入一个索引号，我们就能在这一层生成2^31个私钥
    • 用这一层的Master Chain Code和Master Chain Code以及选取一个固定的索引号作为HMAC-SHA512的输入，又可以得到下一层的Master Private Key以及Master Chain Code，
    • 重复这个递归的过程就可以构造一棵私钥树状结构
    • 这个递归构造的函数我们称之为CKD（child key derivation)函数

  • 6、 CKD (子密钥衍生函数): 这个函数有三个输入

    • 一个母私钥(Master Private Key 256bits)
    • 一个链码(Master Chain code 256 bits)
    • 一个索引号 (32 bits)

这三个输入可以得到一个512bits的输出，在得到一个私钥的同时，也可以作为一棵树的根节点，从而衍生出无数个子密钥。

叶子节点衍生出的子密钥并不能让它发现自己的姊妹密钥，除非你已经有了链码。最初的链码种子（在密码树的根部）是用随机数据构成的，随后链码从各自的母链码中衍生出来。

扩展密钥

正如我们之前看到的，CKD函数可以被用来创造密钥树上任何层级的子密钥。这只需要三个输入量：一个密钥，一个链码以及想要的子密钥的索引。密钥以及链码这两个重要的部分被结合之后，就叫做扩展密钥（extended key）。术语“extended key”也被认为是“可扩展的密钥”，因为这种密钥可以用来衍生子密钥。

引入我们之前的例子，这里我们第一层的扩展密钥为:

1
2
3
4
5
6
7

> from bip32utils import BIP32Key
> from binascii import hexlify
> seed = b'0d756ad408b442341ec4895e854fe5ee55d2a93c6544d3e77b073100e9739e35b897b3fc81ef622babd3f6d7347af2e870d
> root = BIP32Key.fromEntropy(hexlify(seed))
> print(root.ExtendedKey())

xprv9s21ZrQH143K35KaAEjp6RjB4LoeCR3prWBv6vmX7HuGnPFygragV39uDC24D3UZvMnWbhame5nykoXCcfy1Rbgg8uqSzmwoQgFEqt2bUNy

第一层的扩展私钥也被称之为BIP32 Root Key；

得到了一个扩展私钥，就代表得到了树状结构中某个层级的完全控制权，这个扩展密钥可以创造出子密钥并且作为根节点能创造出密钥树结构中的整个分支。分享扩展密钥就可以访问整个分支。

公共子密钥推导

再审视一下前面的CKD函数，第一个输入是一个母私钥(Master Private Key 256bits)，这让我们思考，如果不是输入私钥，而是输入公钥会发生什么呢？

通过母公钥衍生子私钥为分层确定性钱包带来的一个很有用的特点，就是可以不通过私钥而直接从公共母密钥派生出公共子密钥的能力。

因此，扩展密钥可以在HD钱包结构的分支中，被用来衍生所有的公钥（且只有公钥）。

这种快捷方式可以用来创造非常保密的只有公钥配置。在配置中，服务器或者应用程序不管有没有私钥，都可以有扩展公钥的副本。这种配置可以创造出无限数量的公钥以及比特币地址。但是发送到这个地址里的任何比特币都不能使用。与此同时，在另一种更保险的服务器上，扩展私钥可以衍生出所有的对应的可签署交易以及花钱的私钥。

这种方案的常见应用是安装扩展公钥电商的网络服务器上。网络服务器可以使用这个公钥衍生函数去给每一笔交易（比如客户的购物车）创造一个新的比特币地址。但为了避免被偷，网络服务商不会有任何私钥。没有HD钱包的话，唯一的方法就是在不同的安全服务器上创造成千上万个比特币地址，之后就提前上传到电商服务器上。这种方法比较繁琐而且要求持续的维护来确保电商服务器不“用光”公钥。

这种解决方案的另一种常见的应用是冷藏或者硬件钱包。在这种情况下，扩展的私钥可以被储存在纸质钱包中或者硬件设备中（比如 Trezor 硬件钱包），与此同时扩展公钥可以在线保存。使用者可以根据意愿创造“接收”地址而私钥可以安全地在线下被保存。为了支付资金，使用者可以使用扩展的私钥离线签署比特币客户或者通过硬件钱包设备（比如 Trezor）签署交易。下图阐述了扩展母公钥来衍生子公钥的传递机制。

img

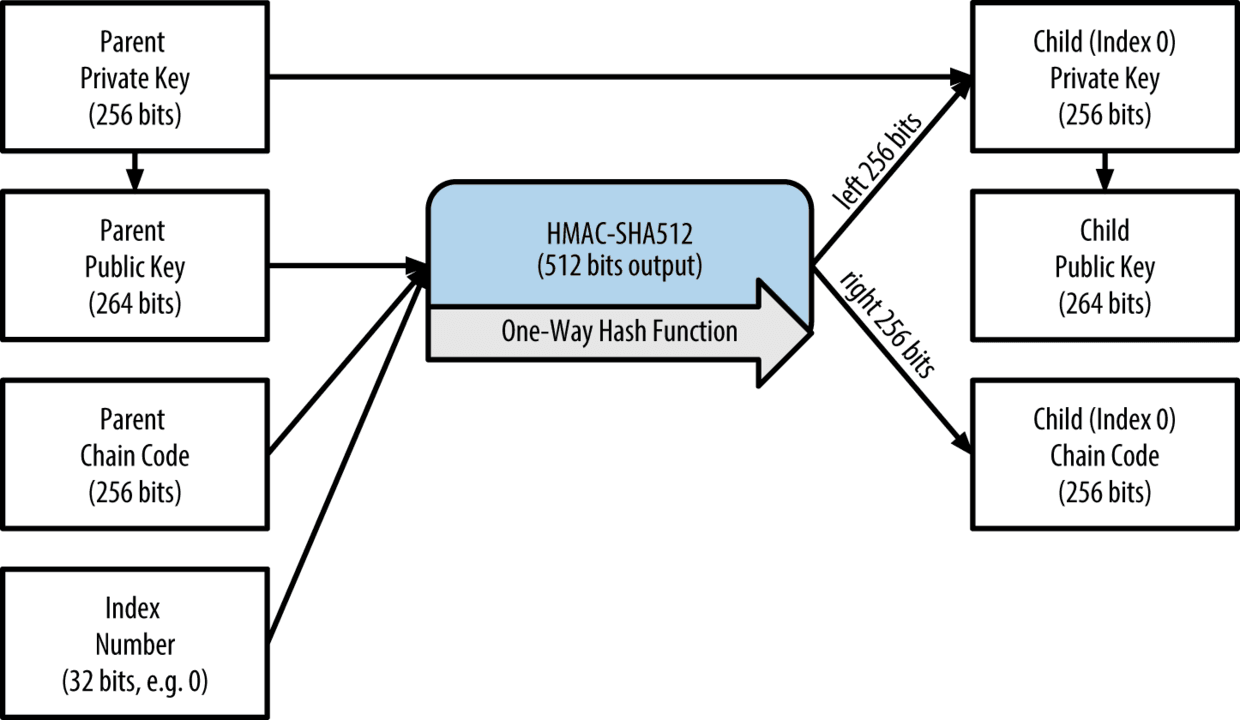
硬化子密钥的衍生

从扩展公钥衍生一个分支公钥的能力是很重要的，但牵扯一些风险。访问扩展公钥并不能得到访问子私钥的途径。但是，因为扩展公钥包含有链码，如果子私钥被知道或者被泄漏的话，链码就可以被用来衍生所有的其他子私钥。简单地泄露的私钥以及一个母链码，可以暴露所有的子密钥。更糟糕的是，子私钥与母链码可以用来推断母私钥。

为了应对这种风险，HD钱包使用一种叫做硬化衍生(hardened derivation）的替代衍生函数。这就“打破”了母公钥以及子链码之间的关系。这个硬化衍生函数使用了母私钥去推导子链码，而不是母公钥。这就在母/子顺序中创造了一道“防火墙”——有链码但并不能够用来推算子链码或者姊妹私钥。强化衍生函数看起来几乎与一般的衍生的子私钥相同，不同的是母私钥被用来输入散列函数中而不是母公钥，如图所示。

img

当强化私钥衍生函数被使用时，得到的子私钥以及链码与使用一般衍生函数所得到的结果完全不同。得到的密钥“分支”可以被用来生产不易被攻击的扩展公钥，因为它所含的链码不能被用来开发或者暴露任何私钥。强化衍生也因此被用在上一层级，使用扩展公钥的密钥树中创造“间隙”。

简单地来说，如果你想要利用扩展公钥的便捷来衍生公钥的分支而不将你自己暴露在泄露扩展链码的风险下， 你应该从强化母私钥衍生公钥，而不是从一般的母私钥来衍生。最好的方式是，为了避免了推到出主密钥，主密钥所衍生的第一层级的子密钥最好使用强化衍生。

正常衍生和强化衍生的索引号码

还记得我们前面说:一个母私钥+索引号，就可以生成2^31个子私钥，2^31是整个2^32范围可用的一半，另一半是做什么的呢？

用在衍生函数中的索引号码是32位的整数。为了区分密钥是从正常衍生函数中衍生出来还是从强化衍生函数中产出，这个索引号被分为两个范围。索引号在0和2^31–1(0x0 to 0x7FFFFFFF)之间的是只被用在常规衍生。索引号在2^31和2^32– 1(0x80000000 to 0xFFFFFFFF)之间的只被用在强化衍生。因此，索引号小于2^31就意味着子密钥是常规的，而大于或者等于2^31的子密钥就是强化型的。

为了让索引号码更容易被阅读和展示，强化子密钥的索引号码是从0开始展示的，但是右上角有一个小撇号。第一个常规子密钥因此被表述为0，但是第一个强化子密钥（索引号为0x80000000）就被表示为0’。第二个强化密钥依序有了索 引号0x80000001，且被显示为1’，以此类推。当你看到HD钱包索引号i’，这就意味着 2^31+i。

HD钱包密钥识别符

我们看到，一个树状的私钥组织，命名就成了一个问题，如何快速的表示这是一个由第三层的第n个扩展子私钥衍生的主密钥呢？

答案是类似于文件路径的命名规则。

每个级别之间用斜杠（/）字符来表示。由主私钥衍生出的私钥起始以“m”打头。由主公钥衍生的公钥起始以“M“打头。因此，母密钥生成的第一个子私钥是m/0。第一个公钥是M/0。第一个子密钥的子密钥就是m/0/1，以此类推。

密钥的“祖先”是从右向左读，直到你达到了衍生出的它的主密钥。举个例子，标识符m/x/y/z描述的是子密钥m/x/y的第z个子密钥。而子密钥m/x/y又是m/x的第y个子密钥。m/x又是m的第x个子密钥。

HD钱包树状结构的导航

HD钱包树状结构提供了极大的灵活性。每一个母扩展密钥有40亿个子密钥：20亿个常规子密钥和20亿个强化子密钥。 而每个子密钥又会有40亿个子密钥并且以此类推。只要你愿意，这个树结构可以无限类推到无穷代。但是，又由于有了这个灵活性，对无限的树状结构进行导航就变得异常困难。尤其是对于在不同的HD钱包之间进行转移交易，因为内部组织到内部分支以及子分支的可能性是无穷的。

两个比特币改进建议（BIPs）提供了这个复杂问题的解决办法——通过创建几个HD钱包树的提议标准。BIP-43提出使用第一个强化子索引作为特殊的标识符表示树状结构的“purpose”。基于BIP-43，HD钱包应该使用且只用第一层级的树的分支，而且有索引号码去识别结构并且有命名空间来定义剩余的树的目的地。举个例子，HD钱包只使用分支m/i’/是 为了表明那个被索引号“i”定义的特殊为目地。

在BIP-43标准下，为了延长的那个特殊规范，BIP-44提议了多账户结构作为“purpose”。所有遵循BIP-44的HD钱包依据只使用树的第一个分支的要求而被定义：m/44’/。 BIP-44指定了包含5个预定义树状层级的结构：

1

m / purpose' / coin_type' / account' / change / address_index

第一层的purpose总是被设定为44’。

第二层的“coin_type”特指币种并且允许多元货币HD钱包中的货币在第二个层级下有自己的亚树状结构。目前有三种货币被定义：Bitcoin is m/44’/0’、Bitcoin Testnet is m/44’/1’，以及 Litecoin is m/44’/2’, Ethereum 是 60’。

树的第三层级是“account”，这可以允许使用者为了会计或者组织目的，而去再细分他们的钱包到独立的逻辑性子账户。 举个例子，一个HD钱包可能包含两个比特币“账户”：m/44’/0’/0’ 和 m/44’/0’/1’。每个账户都是它自己子树的根。

第四层级就是“change”。每一个HD钱包有两个子树，一个是用来接收地址一个是用来创造找零地址。注意无论先前的层级是否使用强化衍生，这一层级使用的都是常规衍生。这是为了允许这一层级的树可以在不安全环境下，输出扩展公钥。

被HD钱包衍生的可用的地址是第四层级的子级，就是第五层级的树的“address_index”。比如，第三个层级的主账户收到比特币支付的地址就是 M/44’/0’/0’/0/2。

几个BIP规范

到这里为止，我们已经了解到了比特币HD钱包的绝大部分构造知识。如果能完全理解了上述内容，我们已经是专家了。让我们再简要回顾一下过程:

  1. 生成一个随机序列作为原始熵
  2. 通过一系列变换操作得到了一个Mnemonic Code，这些操作需要大量的HASH过程，抵御了暴力碰撞。同时，生成的Mnemonic Code作为人类易读的助记词，可以轻易的抄写备份，导入导出，这个Mnemonic Code代表着钱包的完全控制权
  3. 从Mnemonic得到了一个root seed，进而转化为 BIP32 Root Key，这可以构造一棵私钥树的根节点
  4. 从BIP32 Root Key开始，可以构造更多的公共子密钥，或者公共密钥；根据使用场景的不同，可以构造出完全控制的HD钱包，或者离线签署的只读钱包。

这上面一系列的操作细节，被社区总结到了几个BIP规范当中。

BIP32

定义 Hierarchical Deterministic wallet (简称 “HD Wallet”)，是一个系统可以从单一个 seed 产生一树状结构储存多组 keypairs（私钥和公钥）。好处是可以方便的备份、转移到其他相容装置（因为都只需要 seed），以及分层的权限控制等。

BIP39

将 seed 用方便记忆和书写的单字表示。一般由 12 个单字组成，称为 mnemonic code(phrase)，中文称为助记词或助记码。例如：

zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo zoo wrong

BIP43

提出使用第一个强化子索引作为特殊的标识符表示树状结构的“purpose”

BIP44

基于 BIP32和BIP43 的定义，赋予树状结构中的各层特殊的意义。让同一个 seed 可以支持多币种、多帐户等。各层定义如下：

1

m / purpose' / coin_type' / account' / change / address_index

其中的 purporse’ 固定是 44’，代表使用 BIP44。而 coin_type’ 用来表示不同币种，例如 Bitcoin 就是 0’，Ethereum 是 60’。

BIP49，BIP84, BIP141

加入隔离验证后的账户方案

安全性

关于安全性，reddit上面的一个帖子做了比较全面的计算，可以参考。

总结

呼，漫长的一顿操作之后；我们终于拥有了一个完整的HD钱包，它有下面几个特性:

  1. 只要记住seed，即12-24个单词，就可以在不同得系统中导入/导出这个钱包，并掌有完全的控制权，除了知道seed的人，世界上没有任何一个组织能操作这个账户
  2. 这个钱包拥有衍生无数个账户的能力，并通过树状层次组织
  3. 这棵树的任意一个节点都可以衍生出一棵子树，适用于大型组织的财务处理；比如国王拥有根seed的绝对掌控权，他分配了几个一级扩展私钥给总理大臣，而这几个一级扩展私钥又可以作为根节点衍生出二级扩展私钥分配给更多的人…..依次衍生下去无穷无尽，每一级的扩展私钥掌控者都拥有下级的资金调度权力，而同级别的私钥掌控者互不可见；
  4. 通过一个类似于文件系统命名的路径方式，扩展私钥的拥有者可以掌管任意一个子节点的账户，比如将来全家共享一个钱包，父母对子女的零花钱流水账有完全的掌控
  5. 可以构造出一个完全离线的只用来收款而不能付款的钱包账户，用于海量用户的电子商户系统
  6. 可以汇聚多个公私钥体系的电子货币；可以想象，未来所有的电子货币系统都聚集在一个钱包之中

是不是非常神奇的感觉；呼呼，写到这里，我们已经将电子货币系统的钱包设计完全探究了一番；

其实这么长篇大论下来，我想要探讨的真正题目是比特币的交易构成，而不是什么钱包构造。

这个文章3年前就想写了，但是无穷尽的前置知识实在是让人望而却步；目前我们总算是对于比特币的账户系统有所了解了，反正我搞明白之后只能发出感叹：设计的实在是太精巧了；

但是比特币的交易构造之精巧，又胜过钱包十倍。走了这么远的路，还是那句话，还早得很呢。

那么，比特币的交易构造又是怎样的呢？我们下次文章再见。

Comments