2018-11-16 01:40(UTC+8)发生的BCH分叉实在好看,转载一下进程说明:
“分叉前夕: BCH硬分叉过程中:第一个区块由澳本聪阵营svpool爆出,区块大小为51.385KB,区块高度为556761。BCH硬分叉连续爆出6个区块才会正式开始分叉。
BCH硬分叉过程中:第二个区块由澳本聪阵营coingeek爆出,区块大小为8.24kB,区块高度为556762。
BCH硬分叉过程中:第三个区块由澳本聪阵营SVPool爆出,区块大小为29.44kB,区块高度为556763。
在BCH硬分叉过程中,ABC阵营开始反击,比特大陆旗下第一大矿池BTC.com已经获得部分客户同意,切换算力支援BCH ABC。ABC阵营Bitcoin.com矿池的BCH算力在分叉前24小时大增1593.09%,超过澳本聪阵营的Coingeek矿池,排名第一。
BCH硬分叉过程中:第四个区块由吴忌寒阵营Bitcoin.com挖出。区块大小为57.11 kB,区块高度为556764。
BCH硬分叉过程中:第五个区块由吴忌寒阵营ViaBTC爆出,区块大小为315.40 kB,区块高度为556765。
BCH硬分叉过程中:第六个区块由澳本聪阵营SVPool爆出,区块大小为2597.76 kB,区块高度为556766。
区块高度556766:正式分叉。算力大战正式开始。随后比特大陆阵营率先出两个块,并保持持续领先。”
Bitcoin.com矿池临时集了4000P的算力,巅峰时Bitcoin ABC的算力达到了8500P,而Bitcoin SV始终没有超过5000P。分叉当晚,实力差距明显。
https://cash.coin.dance/blocks/hashrate
但是Bitcoin SV目前没有放弃的意思,而且Bitcoin.com抽调的算力会慢慢撤回去,因为SV链没有重放保护,如果一直烧钱维护下去,现在还不能称胜负已分。
Bitcoin SV作为进攻方,按照现在1T算力0.1元/小时的价格计算,每天SV要烧掉$200W 维持这场战争。而且目前在BCH链上挖矿收益绝对小于BTC链,如此烧钱确实是土豪行径。如果CSW始终不加重放保护跟Bitcoin ABC死磕,确实是下决心了。但是如果怂了开始炒作Bitcoin SV,那就说明他也不过是个出来割韭菜的。
但是群众其实也不关心鹿死谁手,反正分叉明朗之前不动就可以了。看戏之余,不妨回顾一下中本聪白皮书中关于51%攻击的计算:
(参考第十一章:计算)
https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system/
这个计算过程还是很有意思的,我们天天听各种媒体讲51%攻击,那么现实世界中,现在确实发生了两方争霸的情况,我们定义几个变量:
- P = 诚实节点制造下一个节点的概率
- Q = 攻击者制造下一个节点的概率
- Qz = 攻击者追上诚实节点z个区块的差距
目前(2018-11-17 17:00 UTC+8)Bitcoin SV链算力4278PH,Bitcoin ABC链算力5677PH,Bitcoin SV落后7个Block。Bitcoin ABC为防守方,Bitcoin SV为进攻方,假如Bitcoin SV就这么死磕到底的话,算力保持不变的情况下,有多大机率能51%攻击呢?如果要提高攻击成功的概率,Bitcoin SV又需要多大的算力呢?
我们又要复习一下概率论里面的ABC了,搬来小方凳,数学课开始~~~~
酒鬼漫步问题
当一个喝大了的酒鬼在路上摇摇晃晃时,你是否会担心他还有能力避开一切障碍,成功找到家门而不是掉到某个下水沟里吗?
实际上,这正是非常有趣的酒鬼漫步问题,不妨让这个酒鬼的处境更夸张一些,设想他站在悬崖边,面前就是万丈深渊。如果他往后退一步远离悬崖的概率是 2/3 , 向前一步靠近悬崖的概率则是 1/3。那他摔下悬崖的概率是多少?
答案肯定不会是简单的 1/3。那不如先来看看酒鬼最初的几步会发生什么。下图是对这个酒鬼最初几步所有可能的轨迹的枚举。
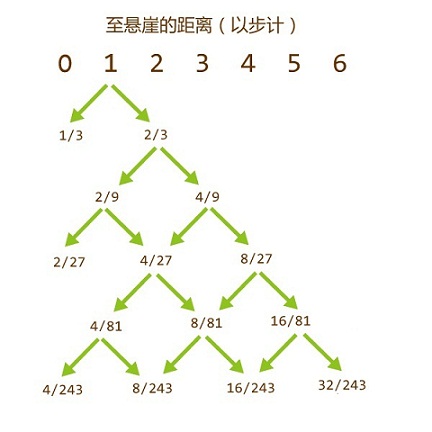
从图中可以看到,达到0 即意味着跌落悬崖。所以在 0 的那些概率的和便是酒鬼前六步掉下悬崖的概率。这个图可以无限推演下去。
所以让我们把这个场景放到数轴上,换一种方式来看。如此一来醉鬼悬崖边漫步就相当于质点沿轴心运动这类问题了。酒鬼在这个数轴上随意地左右走动, 走到 x = 0 的位置意味着被吸收 ,也就是摔下了悬崖。
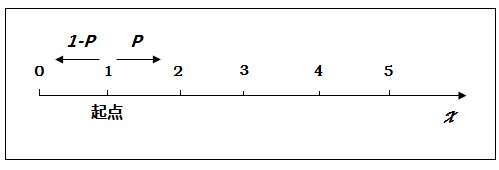
假设他向右一步的概率为 p,向左的概率为 1-p。当他在 x = n(n>0) 的位置的时候,不是向右就是向左。记 P(n)为从 x = n 的位置出发,最后到达 x = 0 被吸收的概率。酒鬼一开始在 x = 1 的位置,我们要求的就是他到 0 的概率。
当酒鬼走完第一步后,他要么到了 x = 0(此事件发生的概率是 1-p),要么到了 x = 2 的位置(此事件发生的概率是 p),他再从 x = 2 出发最终走到 x = 0 被吸收的概率就是 P(2)。这时我们可以得到方程1:
1
| |
而自 x =2 走出并最终到达 x = 0 的情况可以分解为两个阶段:先从 x = 2 到 x = 1(可以走任意步), 然后从 x = 1到 x = 0(同样可以走任意步)。我们知道后一个的概率是 P(1),那么前一个呢?其实是一样的,也是 P(1),它可以看作后一种情况的平移。又因为这两个事件相互独立,所以得到方程2:
1
| |
将方程2代入方程1,得到一个简单的一元二次方程:
1
| |
解得 P(1) = 1 或者 P(1) = (1-p)/p
注意到这里 p 表示的是酒鬼每次向x轴正方向前进一步的概率,也就是他站在悬崖边上向后退的概率。我们不妨根据这个概率的取值情况来对酒鬼悬崖漫步这个问题做个总结。
当 p 等于 0 或 1 时,这显然就成了必然事件,酒鬼一定掉下悬崖或者一定能安全地离开。
但有趣的是,即便当 p 不是 0,在它小于等于 1/2 时,这个酒鬼一样难逃失足的厄运。
当 p = 1/2时, P(1) = 1
众所周知,一个事件发生的概率不会超过 1。所以从上面可以看出,当 p ≤ 1/2时,也就是这个酒鬼每步选择向后退的概率不足一半时,不管他能离开悬崖有多远,最终都必将粉身碎骨。
而如果 p 在 (1/2 , 1) 这个区间里,这时候酒鬼摔落悬崖的概率实际上是一个关于 p 的连续函数。我们可以做出 P(1) 的图像如下
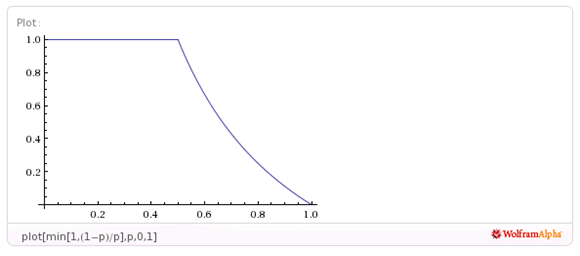
现在让我们回答最初的问题,当酒鬼向后走的概率为2/3时,他摔下悬崖的概率为 1/2 。 很违背直觉的结果,保持一半清醒是不够的,最少要2/3的清醒。
从酒鬼漫步到赌徒破产
把酒鬼徘徊应用到赌博中会得到一个不可思议的结论。假设一个赌徒的赌金是 n,每次的下注金额是 1,而每盘赌局输赢概率各是 1/2。如果一直赌下去的话,赌徒输光的概率是多少呢?
由前面的分析可知,他破产的概率就是前面定义的 P(n)。 P(n)是 P(1) 的 n 次方,而 P(1) 在酒鬼等概率地向两个方向迈步的时候等于 1,所以 P(n)=1 !这告诉我们,即使是公平赌局,你跟赌场玩,最后也一定会输光的!
这就是著名的赌徒破产问题(Gambler’s ruin)。
显然,赌徒的钱越多,输光需要的局数也越多。当赌徒的赌金是 n 时,我们记输光的概率为 p(n)。因为每次赌局有一半的可能赢,一半的可能输,赢的时候赌金变成 n + 1,输的时候变成 n - 1,所以 p(n) = (p(n + 1) + p(n - 1))/2。当 n = 0 的时候,即使不用赌,所有东西也都输光了,所以 p(0) = 1。
由此,p 可以看作一个满足下列递推关系的数列
1 2 3 4 | |
也就是
1
| |
容易验证 p(n) = n * p(1) - (n-1) 正好符合上面的递推关系。
又因为p(n) ≥ 0,所以对于任意的 n,必定有 p(1) ≥ 1 - 1/n。因此 p(1) = 1。那么对于所有的 n,则有 p(n) = 1。这意味着,在无限次的赌博中,赌徒在某一次赌博中输光的概率是 1。
这个发现其实和经典的赌徒谬误异曲同工。上帝创造这个世界的一些规则真是意味深长啊,当你要赌的时候,50%的胜率是不够的,一定要有>50%的把握!
从赌徒破产到算力攻击
将上面两个例子映射到区块链算力争霸的过程中,发现有惊人的相似点。
情况1
当两条分叉从同一起点开始竞争时,就是一个酒鬼漫步问题;攻击者一方相当于不断的要逼近诚实者一方挖出的区块高度;
- 诚实节点:block1——block2——block3——block4——
- 攻击节点:block1——block2A—–block3A—–
攻击节点从block2开始攻击,尝试双花其中的交易,并挖出区块block2A。攻击节点挖出的链要比诚实节点挖出的链长——在本例中,它至少要挖到block5——才算攻击成功。我们把诚实节点的链长度减去攻击节点的链长度,得到的差记为n。诚实节点每挖出一个块则n+1;攻击节点每挖出一个块则n-1。我们把n放到数轴上n-1 ← n → n+1;攻击节点挖出一个块,相当于酒鬼向左移一步;诚实节点挖出一个块,相当于酒鬼向右移一步。设诚实节点领先n个块,如果攻击节点的算力达到或超过了全网的50%,那么它一定能把n减到0。而如果攻击者算力小于50%,则n越大,也就是确认数越多越安全。从这里你们也可以看出来,我们通常所说的51%攻击,是一个没看懂白皮书的人定下的名词。其实应该定名为50%攻击,攻击者不需要大于50%的算力就能成功。
在BCH的分叉战中,如果有一条链的算力一开始能达到算力的50%并保持下去,就可以杀死另外一条链;
情况2
但是随着链的延长,两边的算力便会拉开差距,挖出的快总是有多有少;算力战预测的初始条件变成了这样:
从交易被收录进区块的时候开始,诚实矿工出了z个块。攻击矿工在此期间出块数记为k,只要攻击者不广播别人就不知道,k可能等于0、1、2……直到无穷大。
- 若k>z,攻击直接成功;若k<=z,攻击者仍有可能追上,其成功的可能性即赌徒破产问题。因为攻击失败的情况有限,所以计算成功概率改为计算等价的
1-攻击失败的概率。
首先研究k,假定诚实矿工以均匀的速度出块,则k近似服从泊松分布:P(k, λ);
就是“在一个指定长度的固定区间内有k个点(事件)”的概率。诚实矿工出z块的时间即“指定长度的固定区间”,攻击矿工出块次数k即“事件”,每种k出现的概率是:
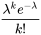
其中λ是攻击矿工出块的期望,假设比特币的算力简化计算为:
速度 * 时间 = 工作量。
z是防御者的工作量,p是防御者的速度,z/p是防御者消耗的时间。防御者的时间=攻击者的时间。攻击者的速度=q;
攻击者的工作量期望 = 攻击者的速度 * 攻击者的时间 = q * z / p 。 即 λ = z*q/p。
根据赌徒破产问题,在落后了z-k个块之后仍旧能追上的概率是:
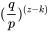
追不上的概率为:
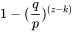
每种k (k<=z)出现的概率,乘以它追不上的概率,就是这个k的失败率:
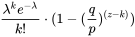
1-所有攻击失败情况的概率之和,就是攻击成功的概率:
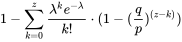
总结
当前Bitcoin SV算力占总算力的43%,落后7个block,取q=0.43, p=0.57, 计算成功率已然小于10%了。
那么,Bitcoin SV要把算力提高到多少,才能有50%的希望追上Bitcoin ABC呢? 这是个复杂的问题啊,首先从分叉一晚的算力战来看,目前BitcoinABC可以调动的算力总量为8500P,所以Bitcoin SV目前一定要调动>8500P的算力,才能有翻盘的机会,至于需要多大才能把翻盘机会搞到50%,课后作业计算吧。
PS:有个小漏洞,因为BCH的难度计算和BTC是不一样的,我不是很确定情况2的计算是否可以假设为泊松分布。
当然,这是一个模拟,真实情况是,发生危机时,bitmain会不断的从BTC那边调集算力过来;这其实是BCH在吸血BTC的算力;
目前来看,BTC的算力有46EH,目前市场上所有的SHA256算力可能总共>60EH;如果算力占再升级,都可以看成是BCH链对BTC链的攻击了。而且只要Bitcoin SV一天不加重放保护,那么交易所就不太可能开放冲提币,这样BCH 链上的交易就会继续停滞,表面上来看是Bitcoin SV一方在烧钱,其实是BCH整条链都在烧钱。现在真正是考验信仰的时候,短期来看,输家会一无所有。赢家也未必能赚到什么。非常残酷的算力战。这真是难得一见,再过10年,真的像中本聪预测的那样,比特币广泛应用后,这种算力战出现的概率极小。某种意义上来说,这个热闹真好看啊:
每天投入$200W的豪赌!
这也进一步验证了,同一个POW算法,最多只能存在一条链,因为即使加了重放保护分叉,还是无法逃脱算力威胁;BCH是一条非常非常特殊的链,它是由bitmain大算力保证的小算力链;这么说可能有点绕口,可以看成BTC和BCH的战争会持续下去,我认为一定会有一方死亡!至于持续多长时间就不好说了,但是我认为这种平衡不可能无限保持下去,必然会发生黑天鹅事件。
另外,像PPC等SHA256 POW币,或者ETC之于ETH,也是同样的情况;我抱持一种观点:
同样的POW算法,如果有大算力存在的情况下,一定归于一条链; 中间可能会多链并存很长时间,但总会发生黑天鹅事件将其它链清零
引用:
https://www.guokr.com/article/59575/?page=3
https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system/
https://www.zhihu.com/question/263764571